Hash的相关知识
Hash又称散列算法、哈希函数,是一种从任何一种数据中创建小的数字“指纹”的方法。散列函数把消息或数据压缩成摘要,使得数据量变小,将数据的格式固定下来。
Hash函数的性质
1.能够根据任意的消息计算出固定长度的Hash值
2.能够快速计算出Hash值
3.消息不同散列值也不同(但是相同的散列值可能来自不同的输入)
4.抗碰撞性:找出任意两个不同的x,x' \in X,使得h(x)=h(x')是困难的(计算不可行);也称强抗碰撞。相对的,也有弱抗碰撞性这个概念。
5.弱抗碰撞性:当给定某条消息的散列值时,单向散列函数必须确保要找到和该条消息具有相同散列值的另外一条消息是非常困难的。
6.强抗碰撞性:是指要找到散列值相同的两条不同的消息是非常困难的。
破解Hash
要从c=hash(m)逆向得到原始明文m,通常有三种办法:
1.暴力攻击法:暴力攻击会尝试每一个在给定长度下各种字符的组合。这种攻击会消耗大量的计算,也通常是破解哈希加密中效率最低的办法,但是它最终会找到正确的密码。因此密码需要足够长,以至于遍历所有可能的字符串组合将耗费太长时间,从而不值得去破解它。
2.查表法:提前构建一个“明文->密文”对应关系的一个大型数据库,破解时通过密文直接反查明文,这也是时间成本最低的一种办法。但存储一个这样的数据库,空间成本是惊人的。
3.彩虹表法:彩虹表是一种在时间和空间的消耗上找寻平衡的破解技术。它和查表法很类似,但是为了使查询表占用的空间更小而牺牲了破解速度。
这三种方法中,彩虹表法是最常用也是最巧妙的方法,下面我们着重讲讲彩虹表法。
彩虹表的前身
在彩虹表之前,已经出现了对哈希函数的破解算法,被称为“预计算的哈希链集”。
这是一条k=2的哈希链(H出现的次数=R出现的次数=2)
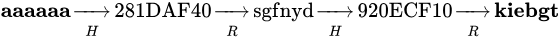
H函数就是要破解的哈希函数。
R函数是构建这条链的时候定义的一个函数:它的值域和定义域与H函数相反。通过该函数可以将哈希值约简为一个与原文相同格式的值。
这条链是这样生成的:
1.随机选择一个明文aaaaaa
2.对其求哈希得到281DAF40
3.R(281DAF40) 得到另外一个明文sgfnyd
4.继续重复2,3步骤
存储的时候,不需要存储所有的节点,只需要存储每条链的头尾节点(这里是aaaaaa和kiebgt)
以大量的随机明文作为起节点,通过上述步骤计算出哈希链并将终节点进行储存,可得到一张哈希链集。
预计算的哈希链集的使用
1.假设其刚好是920ECF10:首先对其进行一次R运算,得到kiebgt,然后发现刚好命中了哈希链集中的(aaaaaa,kiebgt)链条。可以确定其极大概率在这个链条中。于是从aaaaaa开始重复哈希链的计算过程,发现sgfnyd的哈希结果刚好是920ECF10,于是破解成功。
2.密文不是“920ECF10”而是“281DAF40”:第一次R运算后的结果并未在末节点中找到,则再重复一次H运算+R运算,这时又得到了末节点中的值“kiebgt”。于是再从头开始运算,可知aaaaaa刚好可哈希值为281DAF40。
3.如是重复了k(=2)次之后,仍然没有在末节点中找到对应的值,则破解失败。
预计算的哈希链集的意义
对于一个长度为k的预计算的哈希链集,每次破解计算次数不超过k,因此比暴力破解大大节约时间。
每条链只保存起节点和末节点,储存空间只需约1/k,因而大大节约了空间。
理论上每条哈希链可以破解k个哈希值。
可能存在的问题
要发挥预计算的哈希链集的左右,需要一个分布均匀的R函数。当出现碰撞时,就会出现下面这种情况:
111 –H–> EDEDED –R–> 222 –H–> FEDEFE –R–> 333 –H–> FEFEDC –R–> 444
454 –H–> FEDECE –R–> 333 –H–> FEFEDC –R–> 444 -H–> FEGEDC –R–> 555
两条链出现了重叠。这两条哈希链能解密的明文数量就远小于理论上的明文数2×k。由于集合只保存链条的首末节点,因此这样的重复链条并不能被迅速地发现。
彩虹表的改进
彩虹表的出现,针对性的解决了R函数导致的链重叠问题:
它在各步的运算中,并不使用统一的R函数,而是分别使用R1…Rk共k个不同的R函数。
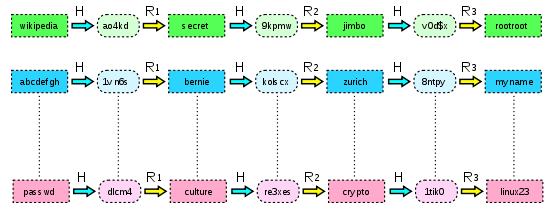
这样一来,即使发生碰撞,也会变成下面的情况:
111 –H–> EDEDED –R1–> 222 –H–> FEDEFE –R2–> 333 –H–> FEFEDC –R3–> 444
454 –H–> FEDECE –R1–> 333 –H–> FEFEDC –R2–> 474 -H–> FERFDC –R3–> 909
即使在极端情况下,两个链条同一序列位置上发生碰撞,导致后续链条完全一致,这样的链条也会因为末节点相同而检测出来,可以丢弃其中一条而不浪费存储空间。
彩虹表的使用
彩虹表的使用比哈希链集稍微麻烦一些。
1.首先,假设要破解的密文位于某一链条的k-1位置处,对其进行Rk运算,看是否能够在末节点中找到对应的值。如果找到,则可以如前所述,使用起节点验证其正确性。
2.否则,继续假设密文位于k-2位置处,这时就需要进行Rk-1、H、Rk两步运算,然后在末节点中查找结果。
3.如是反复,最不利条件下需要将密文进行完整的R1、H、…Rk运算后,才能得知密文是否存在于彩虹表之中。
彩虹表中时间、空间的平衡
对于哈希链集,最大计算次数为k,平均计算次数为k/2
彩虹表的最大计算次数为1+2+3+……k = k(k-1)/2,平均计算次数为[(k+2)*(k+1)]/6。
可见,要解相同个数的明文,彩虹表的代价会高于哈希链集。
无论哈希链集还是彩虹表: 当k越大时,破解时间就越长,但彩虹表所占用的空间就越小; 相反,k越小时,彩虹表本身就越大,相应的破解时间就越短。
彩虹表的抵御
- 最常用的方法就是加盐,这其实是改变了哈希函数H的形式。由于彩虹表在生成和破解的过程中,都反复用到了函数H,H如果发生了改变,则已有的彩虹表数据就完全无法使用,必须针对特定的H重新生成,这样就提高了破解的难度。
- 防御彩虹表的另一种方法是提高H函数的计算难度,例如将H定义为计算一千次MD5后的结果。由于H在算法中的重复性,当单次H函数的计算耗时增加,意味着彩虹表的生成时间会大大的增加,从而也能提高破解的成本。
总结
关于彩虹表,我们容易将其与查表法混淆。认为彩虹表就是依赖查一个巨大的表来破解Hash, 简直是个无知的玩笑。
知乎上的一个比喻很好的解释了这三种破解方法的差异
如果将哈希后的密文比作一把锁,暴力破解的方法就是现场制作各种各样不同齿形的钥匙,再来尝试能否开锁,这样耗时无疑很长;我以前错误理解的“彩虹表”,是事先制作好所有齿形的钥匙,全部拿过来尝试开锁,这样虽然省去了制作钥匙的时间,但是后来发现这些钥匙实在是太多了,没法全部带在身上。而真正的彩虹表,是将钥匙按照某种规律进行分组,每组钥匙中只需要带最有特点的一个,当发现某个“特征钥匙”差一点就能开锁了,则当场对该钥匙进行简单的打磨,直到能开锁为止。这种方法是既省力又省时的。
参考文章:
https://www.zhihu.com/question/19790488/answer/19290308
https://www.jianshu.com/p/732d9d960411